Workflow Steps: Formulation and Sampling

The two main steps of solving problems using quantum computers are:

1. Formulate[1] your problem as an objective function

   An objective function (cost function) is a mathematical expression of the problem to be optimized; for quantum computing, these are quadratic models and (for some hybrid solvers) nonlinear models that have lowest values (energy) for good solutions to the problems they represent.

2. Find good solutions by sampling

   Samplers are processes that sample from low-energy states of objective functions. Find good solutions by submitting your model to one of a variety of D-Wave’s quantum, classical, and hybrid quantum-classical samplers.

Fig. 197 Solution steps: (1) a problem known in “problem space” (a circuit of Boolean gates, a graph, a network, etc) is formulated as a model, mathematically or using Ocean functionality, and (2) the model is sampled for solutions.

[1]

For quantum computing, as for classical, solving a problem requires that it be formulated in a way the computer and its software understand. For example, if you want your laptop to calculate the area of a $1 coin, you might express the problem as an equation, \(A=\pi r^2\), that you program as math.pi*13.245**2 in your Python terminal. For a laptop with Python software, this formulation—a particular string of alphanumeric symbols—causes the manipulation of bits in a CPU and memory chips that produces the correct result.

Objective Functions

To express a problem for a D-Wave solver in a form that enables solution by minimization, you need an objective function, a mathematical expression of the energy of a system. When the solver is a QPU, the energy is a function of binary variables representing its qubits[2]; for quantum-classical hybrid solvers, the objective function might be more abstract[3].

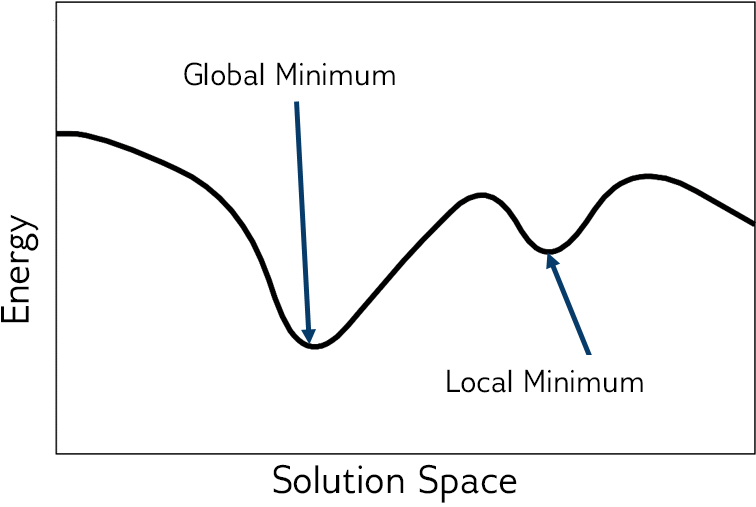
Fig. 198 Energy of the objective function.

For most problems, the lower the energy of the objective function, the better the solution. Sometimes any low-energy state is an acceptable solution to the original problem; for other problems, only optimal solutions are acceptable. The best solutions typically correspond to the global minimum energy in the solution space; see the figure above.

There are many ways of mapping between a problem—chains of amino acids forming 3D structures of folded proteins, traffic in the streets of Beijing, circuits of binary gates—and an objective function to be solved (by sampling) with a D-Wave quantum computer, hybrid solver, or locally on your CPU. The Basic QPU Examples and Basic Hybrid Examples show some simple objective functions to help you begin.

For more detailed information on objective functions, how D-Wave quantum computers minimize objective functions, see the What is Quantum Annealing? section; for techniques for reformulating problems as objective functions, see the Reformulating a Problem section.

For code examples that formulate models for various problems, see D-Wave’s examples repo and many example customer applications on the D-Wave website.

[2]

If you are solving your problem directly on a D-Wave quantum computer, the system is the qubits of a quantum processing unit (QPU) and your objective function represents the states of the qubits as binary variables, and the physical biases and couplings applied to these qubits as, respectively, linear and quadratic coefficients. By formulating an objective function such that lowest energy states represent good solutions to your problem, you can solve your problem by minimizing the objective function. In the case of a D-Wave quantum computer, the QPU uses quantum annealing to seek the minimum of the energy landscape for its qubits with the biases and couplings applied by your objective function.

[3]

For hybrid solvers, some parts of the objective function are minimized using classical heuristics and some by the QPU.

Simple Objective Example

As an illustrative example, consider solving a simple equation, \(x+1=2\), not by the standard algebraic techniques but by formulating an objective that at its minimum value assigns a value to the variable, \(x\), that is also a good solution to the original equation.

Taking the square of the subtraction of one side from another, you can formulate the following objective function to minimize:

\[ \begin{align}\begin{aligned}\text{E}(x) &= [2-(x+1)]^2\\&= (1-x)^2\end{aligned}\end{align} \]

In this case minimization, \(\min_x{(1-x)^2}\), seeks the shortest distance between the sides of the original equation, which occurs at equality (with the square eliminating negative distance).

The Simple Sampling Example example below shows an equally simple solution by sampling.

Supported Models

To express your problem as an objective function and submit to a D-Wave sampler for solution, you typically use one of the Ocean software quadratic models supported by D-Wave quantum computers and some of the Leap service’s hybrid samplers or the nonlinear model.

The following are quadratic models supported on the QPU and some hybrid solvers:

• Binary quadratic models (BQM) are unconstrained and typically represent problems of decisions that could either be true (or yes) or false (no); for example, should an antenna transmit, or did a network node fail? The model uses \(0/1\)-valued variables and \(-1/1\)-valued variables; constraints are typically represented as penalty models.

• Ising models are unconstrained and typically represent problems of decisions that could either be true or or false. The model uses \(-1/1\)-valued variables; constraints are typically represented as penalty models.

• QUBOs are unconstrained and typically represent problems of decisions that could either be true or false. The model uses \(0/1\)-valued variables; constraints are typically represented as penalty models.

The following models are supported only by hybrid solvers:

• Nonlinear models typically represent general optimization problems with an objective function and/or one or more constraints over integer and/or binary variables; the model supports constraints natively.

  This model is especially suited for use with decision variables that represent a common logic, such as subsets of choices or permutations of ordering. For example, in a traveling salesperson problem permutations of the variables representing cities can signify the order of the route being optimized and in a knapsack problem the variables representing items can be divided into subsets of packed and not packed.

• Constrained quadratic models (CQM) are typically used for applications that optimize problems that might include binary-valued variables (both \(0/1\)-valued variables and \(-1/1\)-valued variables), integer-valued variables, and real variables (also known as continuous variables); the model supports constraints natively.

• Discrete quadratic models (DQM) are unconstrained and typically represent problems with several distinct options; for example, which shift should employee X work, or should the state on a map be colored red, blue, green, or yellow? The model uses variables that can represent a set of values such as {red, green, blue, yellow} or {3.2, 67}; constraints are typically represented as penalty models.

Formulation Example: CQM for Greatest Rectangle Area

Consider the simple problem of finding the rectangle with the greatest area when the perimeter is limited.

In this example, the perimeter of the rectangle is set to 8 (meaning the largest area is for the \(2X2\) square). A CQM is created with two integer variables, \(i, j\), representing the lengths of the rectangle’s sides, an objective function \(-i*j\), representing the rectangle’s area (the multiplication of side \(i\) by side \(j\), with a minus sign because Ocean samplers minimize rather than maximize), and a constraint \(2i + 2j <= 8\), requiring that the sum of both sides must not exceed the perimeter .

>>> from dimod import ConstrainedQuadraticModel, Integer
>>> i = Integer('i', upper_bound=4)
>>> j = Integer('j', upper_bound=4)
>>> cqm = ConstrainedQuadraticModel()
>>> cqm.set_objective(-i*j)
>>> cqm.add_constraint(2*i+2*j <= 8, "Max perimeter")
'Max perimeter'

Formulation Example: BQM for a Boolean Circuit

Consider the problem of determining outputs of a Boolean logic circuit. In its original context (in “problem space”), the circuit might be described with input and output voltages, equations of its component resistors, transistors, etc, an equation of logic symbols, multiple or an aggregated truth table, and so on. You can choose to use Ocean software to formulate BQMs for binary gates directly in your code or mathematically formulate a BQM, and both can be done in various ways; for example, a BQM for each gate or one BQM for all the circuit’s gates.

The following are two example formulations.

1. The NOT Gate: Simple QUBO section shows that a NOT gate, represented symbolically as \(x_2 \Leftrightarrow \neg x_1\), is formulated mathematically as BQM,

   \[-x_1 -x_2 + 2x_1x_2\]

2. Ocean software’s dimod package enables the following formulation of an AND gate as a BQM:

>>> from dimod.generators import and_gate
>>> bqm = and_gate('in1', 'in2', 'out')

The BQM for this AND gate may look like this:

>>> bqm     
BinaryQuadraticModel({'in1': 0.0, 'in2': 0.0, 'out': 3.0},
...                  {('in2', 'in1'): 1.0, ('out', 'in1'): -2.0, ('out', 'in2'): -2.0},
...                  0.0,
...                  'BINARY')

The members of the two dicts are linear and quadratic coefficients, respectively, the third term is a constant offset associated with the model, and the fourth shows the variable types in this model are binary.

For more detailed information on the parts of the Ocean software’s programming model and how they work together, see the Ocean Software Stack section.

Once you have a model that represents your problem, you sample it for solutions. The Sampling: Minimizing the Objective subsection explains how to submit your problem for solution.

Sampling: Minimizing the Objective

Having formulated an objective function that represents your problem as described in the Objective Functions subsection above, you sample this quadratic model (QM) or nonlinear model for solutions. Ocean software provides quantum, classical, and quantum-classical hybrid samplers that run either remotely (for example, in the Leap services) or locally on your CPU. These compute resources are known as solvers.

Note

Some classical samplers actually brute-force solve small problems rather than sample, and these are also referred to as “solvers”.

Ocean’s samplers enable you to submit your problem to remote or local compute resources (solvers) of different types:

• Hybrid solvers such as Leap’s service’s hybrid_nonlinear_program_version<x> and hybrid_binary_quadratic_model_version<x> solvers.

• Classical solvers such as the ExactSolver class for exact solutions to small problems

• Quantum solvers such as the Advantage system.

Simple Sampling Example

As an illustrative example, consider solving by sampling the objective, \(\text{E}(x) = (1-x)^2\) found in the Simple Objective Example subsection above to represent equation, \(x+1=2\).

This example creates a simple sampler that generates 10 random values of the variable \(x\) and selects the one that produces the lowest value of the objective:

>>> import random
...
>>> x = [random.uniform(-10, 10) for i in range(10)]
>>> e = list(map(lambda x: (1-x)**2, x))
>>> best_found = x[e.index(min(e))]

One particular execution found this best solution:

>>> print('x_i = ' + ' , '.join(f'{x_i:.2f}' for x_i in x))     
x_i = 7.87, 1.79, 9.61, 2.37, 0.68, -2.93, 3.96, 1.30, -3.85, -0.13
>>> print('e_i = ' + ', '.join(f'{e_i:.2f}' for e_i in e))      
e_i = 47.23, 0.63, 74.19, 1.89, 0.10, 15.44, 8.77, 0.09, 23.50, 1.28
>>> print("Best solution found is {:.2f}".format(best_found))   
Best solution found is 1.30

The figure below shows the value of the objective function for the random values of \(x\) chosen in the execution above. The minimum distance between the sides of the original equation, which occurs at equality, has the lowest value (energy) of \(\text{E}(x)\).

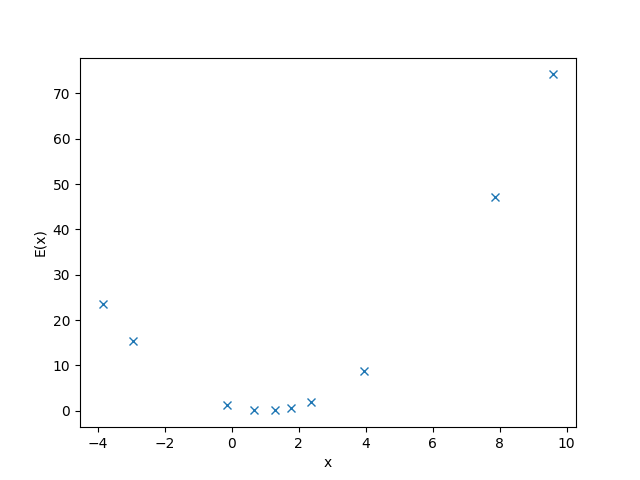
Fig. 199 Values of the objective function, \(\text{E}(x) = (1-x)^2\), versus random values of \(x\) selected by a simple random sampler.

Submit the Model to a Solver

The example code below submits a BQM representing a Boolean AND gate (see also the AND Gate: Minor-Embedding section) to a Leap hybrid solver. In this case, the dwave-system package’s LeapHybridSampler class is the Ocean sampler and the remote compute resource selected might be Leap hybrid solver hybrid_binary_quadratic_model_version<x>.

>>> from dimod.generators import and_gate
>>> from dwave.system import LeapHybridSampler
>>> bqm = and_gate('x1', 'x2', 'y1')
>>> sampler = LeapHybridSampler()    
>>> answer = sampler.sample(bqm)   
>>> print(answer)    
  x1 x2 y1 energy num_oc.
0  1  1  1    0.0       1
['BINARY', 1 rows, 1 samples, 3 variables]

Improve the Solutions

For complex problems, you can often improve solutions and performance by applying some of Ocean software’s preprocessing, postprocessing, and diagnostic tools.

Additionally, when submitting problems directly to a D-Wave quantum computer, you can benefit from some advanced features (for example features such as spin-reversal transforms and anneal offsets, which reduce the impact of possible analog and systematic errors) and the techniques described in the QPU Configuration: Best Practices section.

Example: Preprocessing

The dwave-preprocessing package provides algorithms such as roof duality, which fixes some of a problem’s variables before submitting to a sampler.

As an illustrative example, consider the binary quadratic model, \(x + yz\). Clearly \(x=0\) for all the best solutions (variable assignments that minimize the value of the model) because any assignment of variables that sets \(x=1\) adds a value of 1 compared to assignments that set \(x=0\). (On the other hand, assignment \(y=0, z=0\), assignment \(y=0, z=1\), and assignment \(y=1, z=0\) are all equally good.) Therefore, you can fix variable \(x\) and solve a smaller problem.

>>> from dimod import BinaryQuadraticModel
>>> from dwave.preprocessing import roof_duality
>>> bqm = BinaryQuadraticModel({'x': 1}, {('y', 'z'): 1}, 0,'BINARY')
>>> roof_duality(bqm)
(0.0, {'x': 0})

For problems with hundreds or thousands of variables, such preprocessing can significantly improve performance.

Example: Diagnostics

When sampling directly on the D-Wave QPU, the mapping from problem variables to qubits, minor-embedding, can significantly affect performance. Ocean tools perform this mapping heuristically so simply rerunning a problem might improve results. Advanced users may customize the mapping by directly using the minorminer tool, setting a minor-embedding themselves, or using the problem-inspector tool.

For example, the AND Gate: Minor-Embedding example submits the BQM representing an AND gate to a D-Wave quantum computer, which requires mapping the problem’s logical variables to qubits on the QPU. The code below invokes the problem-inspector tool to visualize the minor-embedding.

>>> import dwave.inspector
>>> dwave.inspector.show(response)   

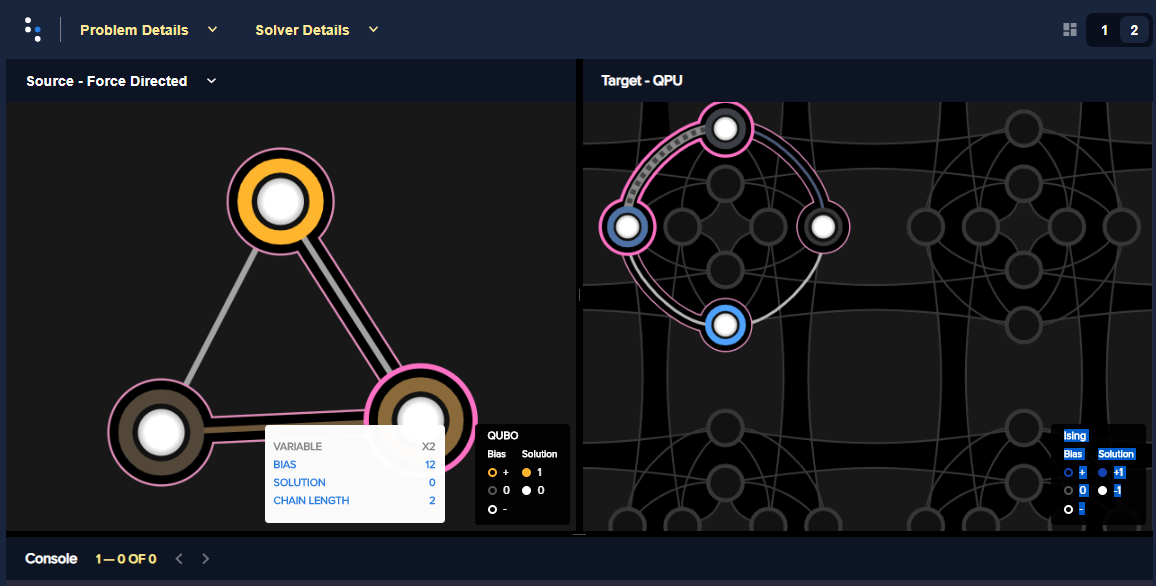
Fig. 200 View of the logical and embedded problem rendered by Ocean’s problem inspector. The AND gate’s original BQM is represented on the left; its embedded representation on a D-Wave system, on the right, shows a two-qubit chain (qubits 176 and 180) for variable \(x2\). The tool is helpful in visualizing the quality of your embedding.

See also the Inspecting Minor-Embeddings section.

Example: Postprocessing

Example Postprocessing with a Greedy Solver improves samples returned from a QPU by post-processing with a classical greedy algorthim.

See also the Postprocessing section.