Algorithms#
Implementations of graph-theory algorithms on the D-Wave system and other binary quadratic model samplers.
Canonicalization#
|
Returns a mapping from the labels of G to chimera-indexed labeling. |
Clique#
A clique in an undirected graph G = (V, E) is a subset of the vertex set such that for every two vertices in C there exists an edge connecting the two.
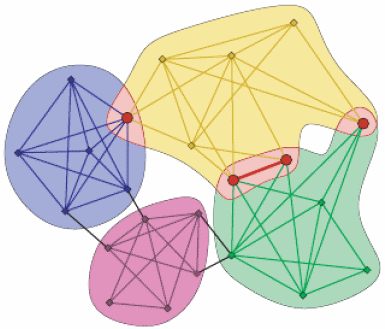
|
Returns an approximate maximum clique. |
|
Returns the number of vertices in the maximum clique of a graph. |
|
Determines whether the given nodes form a clique. |
Coloring#
Graph coloring is the problem of assigning a color to the vertices of a graph in a way that no adjacent vertices have the same color.
Example#
The map-coloring problem is to assign a color to each region of a map (represented by a vertex on a graph) such that any two regions sharing a border (represented by an edge of the graph) have different colors.
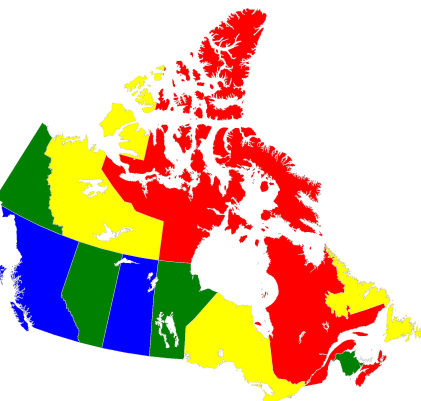
Fig. 211 Coloring a map of Canada with four colors.#
|
Determines whether the given coloring is a vertex coloring of graph G. |
|
Returns an approximate minimum vertex coloring. |
|
Return a QUBO with ground states corresponding to a minimum vertex coloring. |
|
Returns an approximate vertex coloring. |
|
Return the QUBO with ground states corresponding to a vertex coloring. |
Cover#
Vertex covering is the problem of finding a set of vertices such that all the edges of the graph are incident to at least one of the vertices in the set.
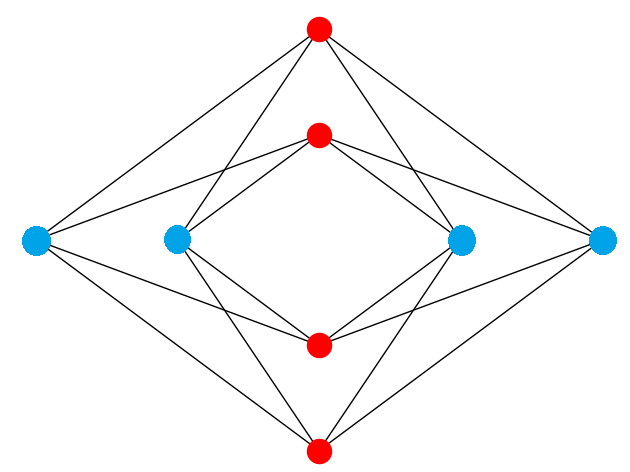
Fig. 212 Cover for a Chimera unit cell: the nodes of both the blue set of vertices (the horizontal tile of the Chimera unit cell) and the red set (vertical tile) connect to all 16 edges of the graph.#
|
Determines whether the given set of vertices is a vertex cover of graph G. |
|
Returns an approximate minimum weighted vertex cover. |
|
Returns an approximate minimum vertex cover. |
Elimination Ordering#
Many algorithms for NP-hard problems are exponential in treewidth. However, finding a lower bound on treewidth is in itself NP-complete. [Gog2004] describes a branch-and-bound algorithm for computing the treewidth of an undirected graph by searching in the space of perfect elimination ordering of vertices of the graph.
A clique of a graph is a fully-connected subset of vertices; that is, every pair of vertices in the clique share an edge. A simplicial vertex is one whose neighborhood induces a clique. A perfect elimination ordering is an ordering of vertices \(1..n\) such that any vertex \(i\) is simplicial for the subset of vertices \(i..n\).
|
Provides a variable elimination order for a Chimera graph. |
|
Calculates the width of the tree decomposition induced by a variable elimination order. |
|
Determines whether a node n in G is almost simplicial. |
|
Determines whether a node n in G is simplicial. |
Computes an upper bound on the treewidth of graph G based on the max-cardinality heuristic for the elimination ordering. |
|
Computes a lower bound for the treewidth of graph G. |
|
Computes an upper bound on the treewidth of graph G based on the min-fill heuristic for the elimination ordering. |
|
Computes an upper bound on the treewidth of graph G based on the min-width heuristic for the elimination ordering. |
|
|
Provides a variable elimination order for the Pegasus graph. |
|
Computes the treewidth of graph G and a corresponding perfect elimination ordering. |
Markov Networks#
|
Samples from a markov network using the provided sampler. |
Construct a binary quadratic model for a markov network. |
Matching#
A matching is a subset of graph edges in which no vertex occurs more than once.
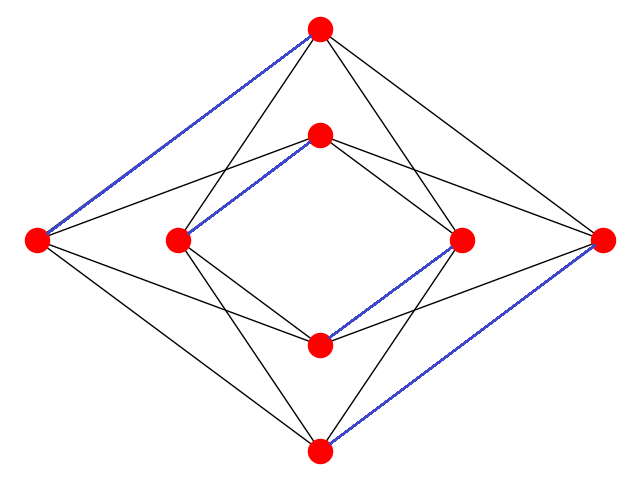
Fig. 213 A matching for a Chimera unit cell: no vertex is incident to more than one edge in the set of blue edges#
|
Find a binary quadratic model for the graph's matchings. |
|
Find a binary quadratic model for the graph's maximal matchings. |
|
Find a binary quadratic model for the graph's minimum maximal matchings. |
|
Returns an approximate minimum maximal matching. |
Maximum Cut#
A maximum cut is a subset of a graph’s vertices such that the number of edges between this subset and the remaining vertices is as large as possible.
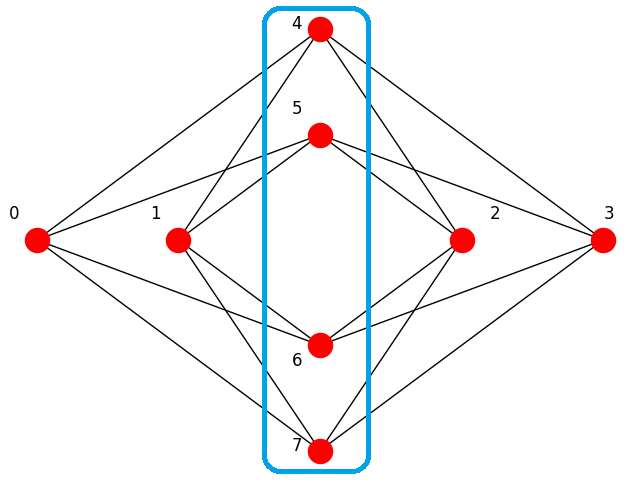
Fig. 214 Maximum cut for a Chimera unit cell: the blue line around the subset of nodes {4, 5, 6, 7} cuts 16 edges; adding or removing a node decreases the number of edges between the two complementary subsets of the graph.#
|
Returns an approximate maximum cut. |
|
Returns an approximate weighted maximum cut. |
Independent Set#
An independent set is a set of a graph’s vertices with no edge connecting any of its member pairs.

Fig. 215 Independent sets for a Chimera unit cell: the nodes of both the blue set of vertices (the horizontal tile of the Chimera unit cell) and the red set (vertical tile) are independent sets of the graph, with no blue node adjacent to another blue node and likewise for red nodes.#
|
Returns an approximate maximum weighted independent set. |
|
Returns an approximate maximum independent set. |
|
Determines whether the given nodes form an independent set. |
Helper Functions#
|
Return the QUBO with ground states corresponding to a maximum weighted independent set. |
Partitioning#
A k-partition consists of k disjoint and equally sized subsets of a graph’s vertices such that the total number of edges between nodes in distinct subsets is as small as possible.
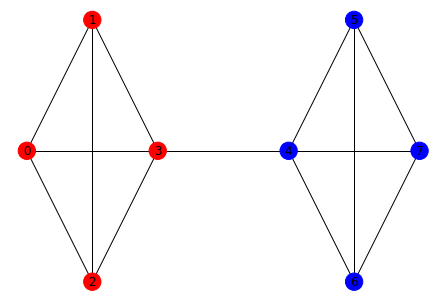
Fig. 216 A 2-partition for a simple graph: the nodes in blue are in the ‘0’ subset, and the nodes in red are in the ‘1’ subset. There are no other arrangements with fewer edges between two equally sized subsets.#
|
Returns an approximate k-partition of G. |
Traveling Salesperson#
A traveling salesperson route is an ordering of the vertices in a complete weighted graph.
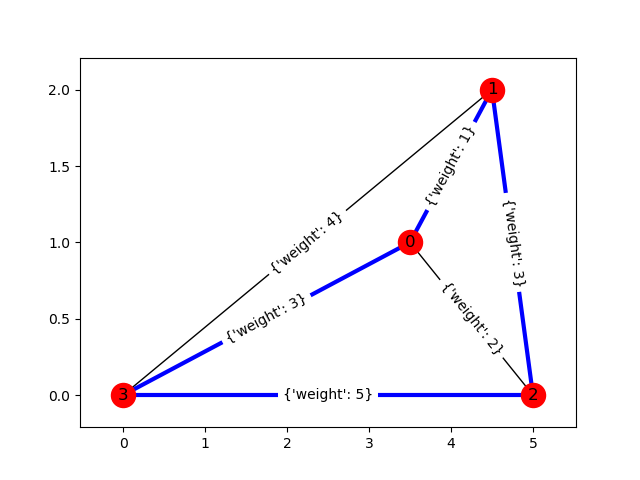
Fig. 218 A traveling salesperson route of [2, 1, 0, 3].#
|
Returns an approximate minimum traveling salesperson route. |
|
Return the QUBO with ground states corresponding to a minimum TSP route. |
Social#
A signed social network graph is a graph whose signed edges represent friendly/hostile interactions between vertices.
Fig. 217 A signed social graph for three nodes, where Eve and Bob are friendly with each other and hostile to Alice. This network is balanced because it can be cleanly divided into two subsets, {Bob, Eve} and {Alice}, with friendly relations within each subset and only hostile relations between the subsets.#
structural_imbalance(S[, sampler])Returns an approximate set of frustrated edges and a bicoloring.
structural_imbalance_ising(S)Construct the Ising problem to calculate the structural imbalance of a signed social network.