Minor Embedding#
To solve an arbitrarily structured
binary quadratic model (BQM) directly on a
D-Wave quantum computer requires mapping, called minor embedding, to
the topology of the system’s quantum processing unit
(QPU). This preprocessing can be done by a composed sampler consisting
of the DWaveSampler() and a composite that
performs minor-embedding. (This step is handled automatically by hybrid
samplers such as LeapHybridSampler.)
For example, a simple two-variable BQM,
might be embedded to two connected qubits, such as 633 and 3603 on the
particular Advantage system shown below:

Fig. 47 Two-variable problem, shown on the left as a graph, is embedded in two
connected qubits on an Advantage, shown on the right against the Pegasus
topology. Variable \(s_0\), highlighted in dark magenta, is represented
by qubit number 633 and variable \(s_1\) is represented by qubit
3603. (This and similar images in this section are generated by Ocean’s
problem inspector tool.)#
In the Advantage’s Pegasus topology, most qubits are connected to
fifteen other qubits, so other valid minor-embeddings for this particular QPU
might be 633 for \(s_0\) and 634 for \(s_1\) or 4628 for
\(s_0\) and 1749 for \(s_1\).
Chains#
Larger problems often require chains because the QPU topology is not fully connected. For example, a \(K_5\) graph is not native to the Pegasus topology, meaning that the following five-variable BQM with a clique (fully-connected) \(K_5\) graph cannot be represented by five qubits on an Advantage QPU.
>>> import dimod
>>> bqm = dimod.generators.doped(1, 5)
>>> bqm.add_linear_from({v: 1 for v in bqm.variables})
Instead, at least one variable is represented by a chain of physical qubits, as in this minor-embedding:

Fig. 48 Five-variable \(K_5\) fully-connected problem, shown on the left as a
graph, is embedded in six qubits on an Advantage, shown on the right against
the Pegasus topology. Variable 0, highlighted in dark magenta, is
represented by two qubits, 1975 and 4840.#
The minor-embedding above was derived from the hueristic used by the
EmbeddingComposite composite on the
working graph of an Advantage selected by the
DWaveSampler sampler class:
>>> from dwave.system import DWaveSampler, EmbeddingComposite, FixedEmbeddingComposite
>>> sampler = EmbeddingComposite(DWaveSampler())
Other qubits might have been chosen; for example,
>>> sampler = FixedEmbeddingComposite(DWaveSampler(),
... embedding={0: [4408, 2437], 1: [4333], 2: [4348], 3: [2497], 4: [2512]})
intentionally sets the embedding shown below to represent this same \(K_5\) graph:
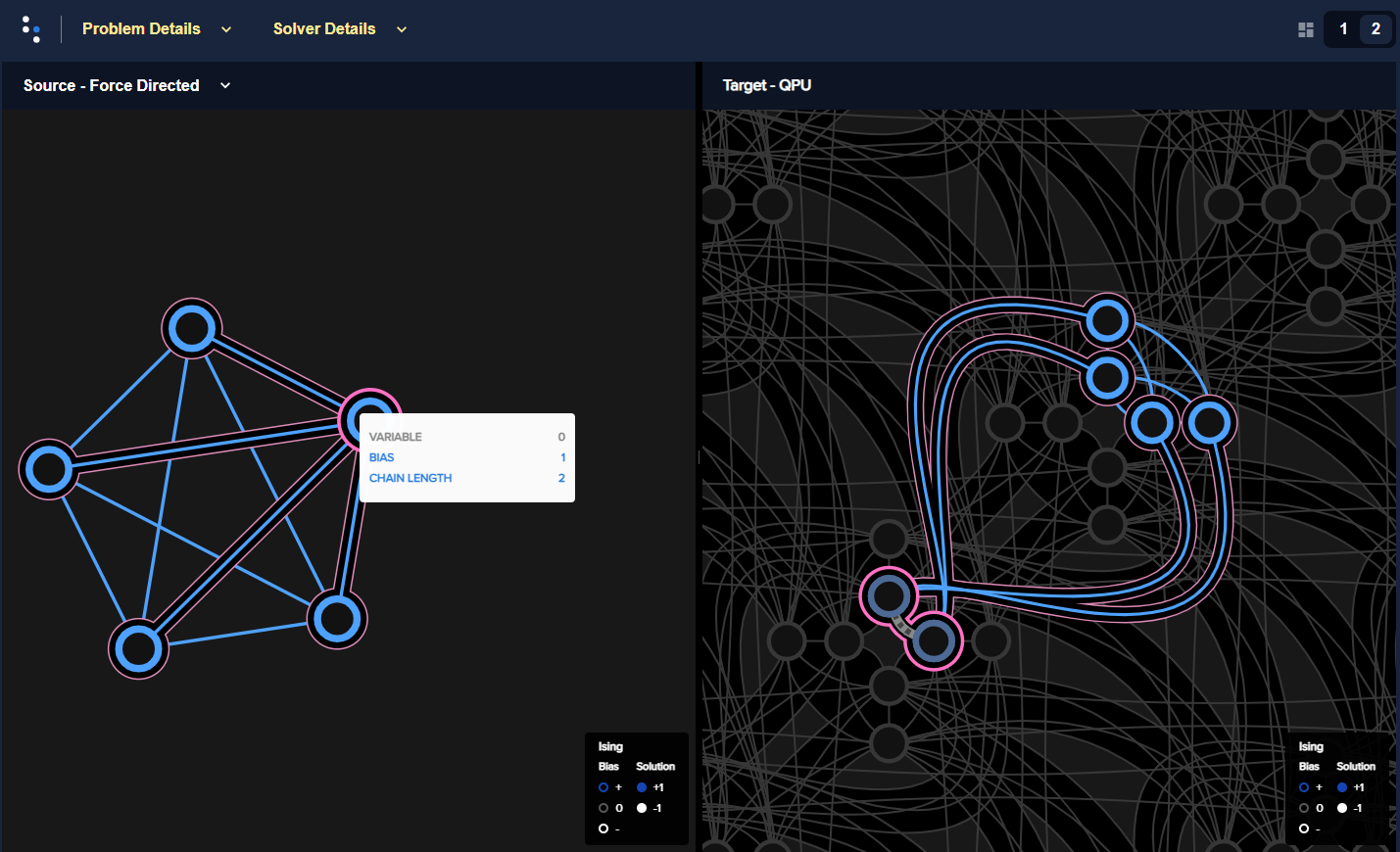
Fig. 49 Five-variable \(K_5\) fully-connected problem, shown on the left as a
graph, is embedded in six qubits on an Advantage, shown on the right against
the Pegasus topology. Variable 0, highlighted in dark magenta, is
represented by two qubits, 4408 and 2437.#
Chain Strength#
For a chain of qubits to represent a variable, all its constituent qubits must return the same value for a sample. This is accomplished by setting a strong coupling to the edges connecting these qubits. That is, for the qubits in a chain to be likely to return identical values, the coupling strength for their connecting edges must be strong compared to the coupling with other qubits that influence non-identical outcomes.
The \(K_5\) BQM for a dimod
doped(), created in the
subsection above, has ten
ground states (best solutions). These are shown
below—solved by brute-force stepping through all possible configurations of
values for the variables—with ground-state energy \(-3.0\):
>>> print(dimod.ExactSolver().sample(bqm).lowest())
0 1 2 3 4 energy num_oc.
0 +1 +1 -1 -1 -1 -3.0 1
1 -1 +1 +1 -1 -1 -3.0 1
2 +1 -1 +1 -1 -1 -3.0 1
3 -1 -1 +1 +1 -1 -3.0 1
4 -1 +1 -1 +1 -1 -3.0 1
5 +1 -1 -1 +1 -1 -3.0 1
6 -1 -1 -1 +1 +1 -3.0 1
7 -1 -1 +1 -1 +1 -3.0 1
8 -1 +1 -1 -1 +1 -3.0 1
9 +1 -1 -1 -1 +1 -3.0 1
['SPIN', 10 rows, 10 samples, 5 variables]
These solutions are states in which two variables are assigned one value and the remaining three variables the complementary value; for example two are \(-1\) and three \(+1\) as shown below.
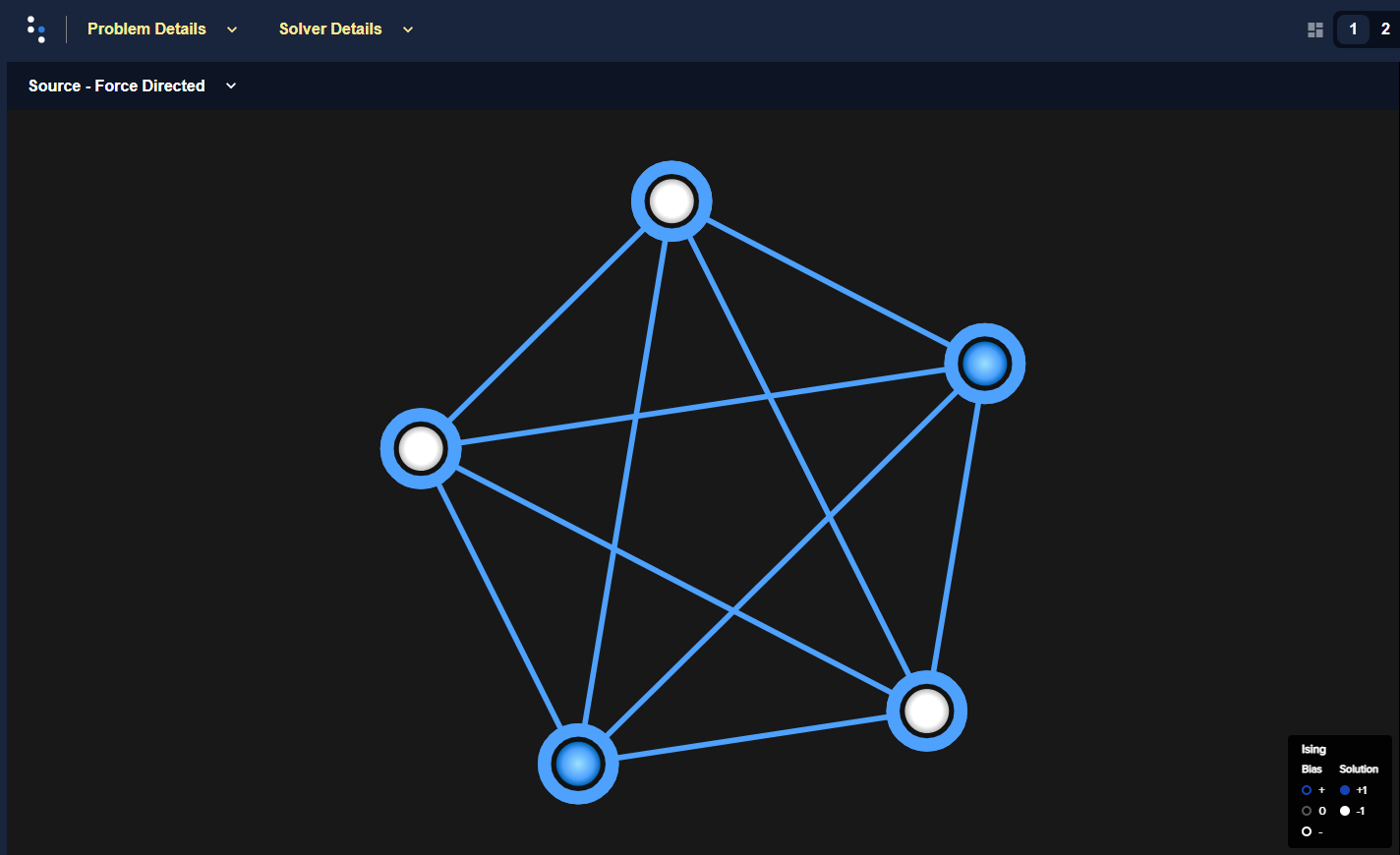
Fig. 50 Ground state of the five-variable \(K_5\) fully-connected problem.#
A typical submission of the problem to a quantum computer, using the same minor-embedding as the previous subsection and the default chain strength, returned all the ground states, with these solutions constituting over 90% of the returned samples.
>>> sampleset = sampler.sample(bqm, num_reads=1000)
>>> print(sampleset.lowest())
0 1 2 3 4 energy num_oc. chain_.
0 -1 +1 +1 -1 -1 -3.0 69 0.0
1 +1 -1 -1 +1 -1 -3.0 115 0.0
2 +1 -1 -1 -1 +1 -3.0 95 0.0
3 +1 -1 +1 -1 -1 -3.0 84 0.0
4 -1 -1 -1 +1 +1 -3.0 116 0.0
5 -1 -1 +1 +1 -1 -3.0 99 0.0
6 -1 -1 +1 -1 +1 -3.0 91 0.0
7 +1 +1 -1 -1 -1 -3.0 71 0.0
8 -1 +1 -1 +1 -1 -3.0 98 0.0
9 -1 +1 -1 -1 +1 -3.0 95 0.0
10 +1 -1 -1 +1 -1 -3.0 1 0.2
['SPIN', 11 rows, 934 samples, 5 variables]
The default chain strength is set by the
uniform_torque_compensation() function:
>>> print(round(sampleset.info['embedding_context']['chain_strength'], 3))
2.828
Resubmitting with a much lower chain strength produced less satisfactory results (only ~10% of returned samples are ground states).
>>> sampleset = sampler.sample(bqm, num_reads=1000, chain_strength=1)
>>> print(sampleset.lowest())
0 1 2 3 4 energy num_oc. chain_.
0 -1 +1 +1 -1 -1 -3.0 12 0.0
1 +1 -1 -1 +1 -1 -3.0 13 0.0
2 +1 -1 -1 -1 +1 -3.0 13 0.0
3 +1 -1 +1 -1 -1 -3.0 16 0.0
4 -1 -1 -1 +1 +1 -3.0 6 0.0
5 -1 -1 +1 +1 -1 -3.0 10 0.0
6 -1 -1 +1 -1 +1 -3.0 17 0.0
7 +1 +1 -1 -1 -1 -3.0 17 0.0
8 -1 +1 -1 +1 -1 -3.0 10 0.0
9 -1 +1 -1 -1 +1 -3.0 7 0.0
['SPIN', 10 rows, 121 samples, 5 variables]
Many of the remaining ~90% of returned samples have “broken chains”, meaning qubits of a chain did not have identical values due to insufficiently strong coupling compared to quadratic coefficients of interactions (of the variable the chain represented) with other variables.
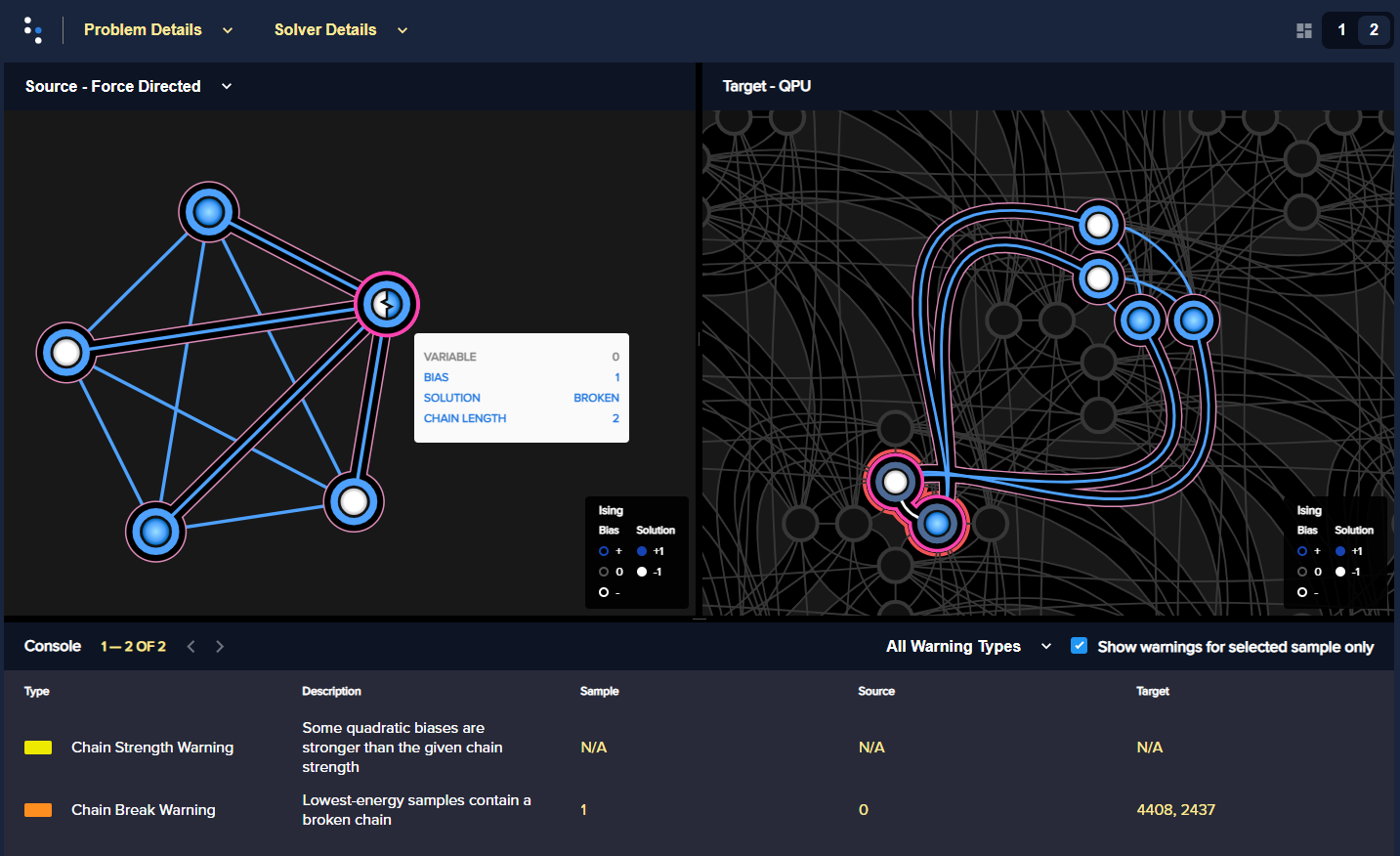
Fig. 51 Five-variable \(K_5\) fully-connected problem is embedded in six qubits
on an Advantage using a low chain strength. Variable 0, highlighted in
dark magenta, is represented by two qubits, numbers 2437 and 4408.
The displayed solution has a broken chain: qubit 4408 returned a value
of \(-1\) (represented by a white dot) while qubit 2347 returned a
value of \(+1\) (a blue dot). The logical representation of the problem,
on the left, shows a half-white, half-blue dot to represent a value based on
a broken chain.#
Further Information#
For information on handling embedding and chains, see the following sections:
Section Minor-Embedding: Best Practices provides more-advanced guidance.
Examples in the AND Gate: Minor-Embedding, Logic Circuit: Embedding Effects, and Using the Problem Inspector sections show through some simple examples how to embed and set chain strength.
The minorminer tool is the hueristic used by common Ocean embedding composites.
The problem inspector tool visualizes embeddings.