Constraint Satisfaction Problem#
A constraint satisfaction problem (CSP) requires that all the problem’s variables be assigned values, out of a finite domain, that result in the satisfying of all constraints.
The map-coloring CSP, for example, is to assign a color to each region of a map such that any two regions sharing a border have different colors.
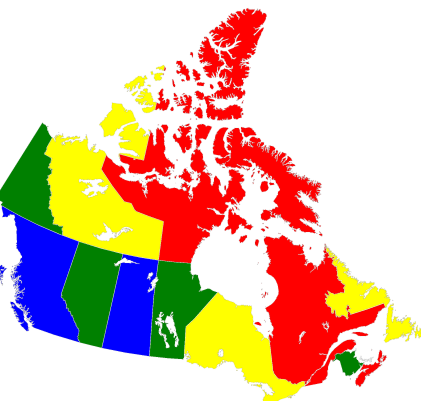
Fig. 226 Coloring a map of Canada with four colors.#
The constraints for the map-coloring problem can be expressed as follows:
Each region is assigned one color only, of C possible colors.
The color assigned to one region cannot be assigned to adjacent regions.
A finite domain CSP consists of a set of variables, a specification of the domain of each variable, and a specification of the constraints over combinations of the allowed values of the variables. A constraint Cα(xα) defined over a subset of variables xα defines the set of feasible and infeasible combinations of xα. The constraint Cα may be be viewed as a predicate which evaluates to true on feasible configurations and to false on infeasible configurations. For example, if the domains of variables X1,X2,X3 are all {0,1,2}, and the constraint is X1+X2<X3 then the feasible set is {(0,0,1),(0,0,2),(0,1,2),(1,0,2)}, and all remaining combinations are infeasible.
Binary CSPs#
Solving such problems as the map-coloring CSP on a sampler such as the D-Wave quantum computer necessitates that the mathematical formulation use binary variables because the solution is implemented physically with qubits, and so must translate to spins si∈{−1,+1} or equivalent binary values xi∈{0,1}. This means that in formulating the problem by stating it mathematically, you might use unary encoding to represent the C colors: each region is represented by C variables, one for each possible color, which is set to value 1 if selected, while the remaining C−1 variables are 0.
Another example is logical circuits. Logic gates such as AND, OR, NOT, XOR etc can be viewed as binary CSPs: the mathematically expressed relationships between binary inputs and outputs must meet certain validity conditions. For inputs x1,x2 and output y of an AND gate, for example, the constraint to satisfy, y=x1x2, can be expressed as a set of valid configurations: (0, 0, 0), (0, 1, 0), (1, 0, 0), (1, 1, 1), where the variable order is (x1,x2,y).
x1,x2 |
y |
|---|---|
0,0 |
0 |
0,1 |
0 |
1,0 |
0 |
1,1 |
1 |
You can use Ocean’s dwavebinarycsp to construct a BQM from a CSP. It maps each individual constraint in the CSP to a “small” Ising model or QUBO, in a mapping called a penalty model.