Traveling Salesperson: Simple Nonlinear Model#

This example demonstrates the most basic use of a Leap hybrid solver on a problem formulated as a nonlinear model. For more-advanced solver usage, see the Vehicle Routing: Using a Nonlinear Model section; for information on formulating problems as nonlinear models, see the Model Construction (Nonlinear Models) section.

The goal of renowned traveling salesperson optimization problem is, for a given a list of cities and distances between each pair of cities, to find the shortest possible route that visits each city exactly once and returns to the city of origin.

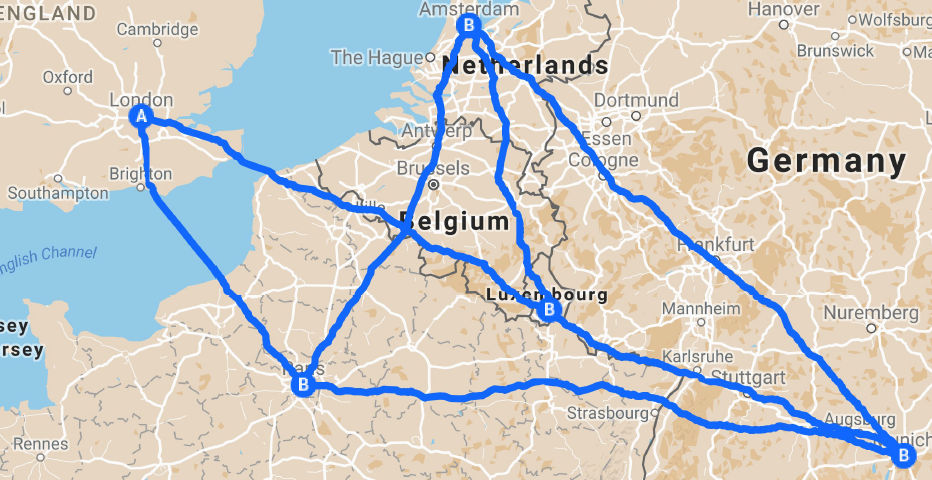
Fig. 19 Traveling-salesperson problem. Map data © 2017 GeoBasis-DE/BKG (© 2009), Google.#

Example Requirements#

The code in this example requires that your development environment have Ocean software and be configured to access SAPI, as described in the Configuring Access to the Leap Service (Basic) section.

Solution Steps#

Basic Workflow: Models and Sampling describes the problem-solving workflow as consisting of two main steps: (1) Formulate the problem as an objective function in a supported model and (2) Solve your model with a D-Wave solver.

This example formulates this problem as a nonlinear model and uses the LeapHybridNLSampler class to find good solutions.

Formulate the Problem#

First, create a matrix of distances between all pairs of the problem’s destinations. In real-world problems, such a matrix can be generated from an application with access to an online map. Here a matrix of approximate driving distances between five Italian cities is created with the following index order: 0: Rome, 1: Turin, 2: Naples, 3: Milan, and 4: Genoa.

>>> DISTANCE_MATRIX = [
...     [0, 656, 227, 578, 489],
...     [656, 0, 889, 141, 170],
...     [227, 889, 0, 773, 705],
...     [578, 141, 773, 0, 161],
...     [489, 170, 705, 161, 0]]

For example, the distance between Turin (row 1) and Milan (column 3) is about 141 kilometers. Note that such a distance matrix is symmetric because the distance between Rome to Turin is the same regardless of the direction of travel.

This example uses one of Ocean software’s model generators to instantiate a Model class for a traveling-salesperson problem. The Model class encodes all the information (objective function, constraints, constants, and decision variables) relevant to your models.

>>> from dwave.optimization.generators import traveling_salesperson
>>> model = traveling_salesperson(distance_matrix=DISTANCE_MATRIX)

For detailed information on how the traveling-salesperson problem is modelled, see the documentation for the traveling_salesperson generator.

Solve the Problem by Sampling#

The Leap quantum cloud service provides hybrid solvers you can submit your models to. These solvers, which implement state-of-the-art classical algorithms together with intelligent allocation of the quantum processing unit (QPU) to parts of the problem where it benefits most, are designed to accommodate even very large problems. The Leap services’solvers can relieve you of the burden of any current and future development and optimization of hybrid algorithms that best solve your problem.

Ocean software’s dwave-system LeapHybridNLSampler class enables you to easily incorporate Leap’s hybrid nonlinear-model solvers into your application:

>>> from dwave.system import LeapHybridNLSampler
>>> sampler = LeapHybridNLSampler()                  

Submit the model to the selected solver.

>>> results = sampler.sample(
...     model,
...     label='SDK Examples - TSP')     

The traveling_salesperson generator constructs a model with a single decision variable to represent the itinerary; the code below iterates through the model’s decision variables, in effect retrieving the variable used by the model to represent the itinerary. It prints the first state set by the solver, which represents an assigned travel order for the five Italian cities (Milan, Rome, Naples, Turin, Genoa).

>>> route, = model.iter_decisions()     
>>> print(route.state(0))               
[3. 0. 2. 1. 4.]

For more advanced usage of the results returned by the solver, see the Vehicle Routing: Using a Nonlinear Model section